Dynamics of Structures

Chapter 4. Response of SDOF to General Dynamic Loading

Chapter 4
4.1 General Dynamic Excitation4.2 Numerical Solution of the Equation of Motion 4.3 Examples

4.2 Numerical Solution of the Equation of Motion

Figure 4.2.1 Piecewise Linear Load

We have seen how Duhamel's integral can be very helpful in providing a closed form solution for the equation of motion. For many practical cases, the type of load is not as simple as we have seen in the previous section. In the more complex cases, numerical methods are normally used to solve the equation of motion. The method that we will present here is exact for a general loading function that can be modeled by piecewise linear segments. It will provide excellent results as long as the time step is chosen to be small enough to capture all the critical points in the loading function.

Representing the Excitation by a linear function

Any arbitrary excitation the system can be subjected to can be descritized using a picewise function as follows,

F(τ)=Fi+(ΔFiΔt)τ F(\tau) = F_i + \Big(\frac{\Delta F_i}{\Delta t} \Big) \tau

Eq. 4.2.1

Where,

ΔFi=Fi+1−Fi \Delta F_i = F_{i+1} - F_i

Eq. 4.2.2

And,

Δti=ti+1−ti \Delta t_i = t_{i+1} - t_i

Eq. 4.2.3

The equation of motion becomes,

mu¨+cu˙+ku=Fi+(ΔFiΔt)τ m \ddot{u} + c \dot{u} + k u = F_i + \Big(\frac{\Delta F_i}{\Delta t} \Big) \tau

Eq. 4.2.4

After some algebra, recurrence formulas for the displacment, velocity and accelerations can be obtained as follows,

ui+1=A ui+Bu˙i+C Fi+D Fi+1 u_{i+1} = A \ u_i + B \dot{u}_i + C \ F_i + D \ F_{i+1}

Eq. 4.2.5

u˙i+1=A′ui+B′u˙i+C′Fi+D′Fi+1 \dot{u}_{i+1} = A' u_i + B' \dot{u}_i + C' F_i + D' F_{i+1}

Eq. 4.2.6

u¨i+1=1m(Fi+1−cu˙i+1−kui+1) \ddot{u}_{i+1} = \frac{1}{m} \Big(F_{i+1} - c \dot{u}_{i+1} - k u_{i+1} \Big)

Eq. 4.2.7

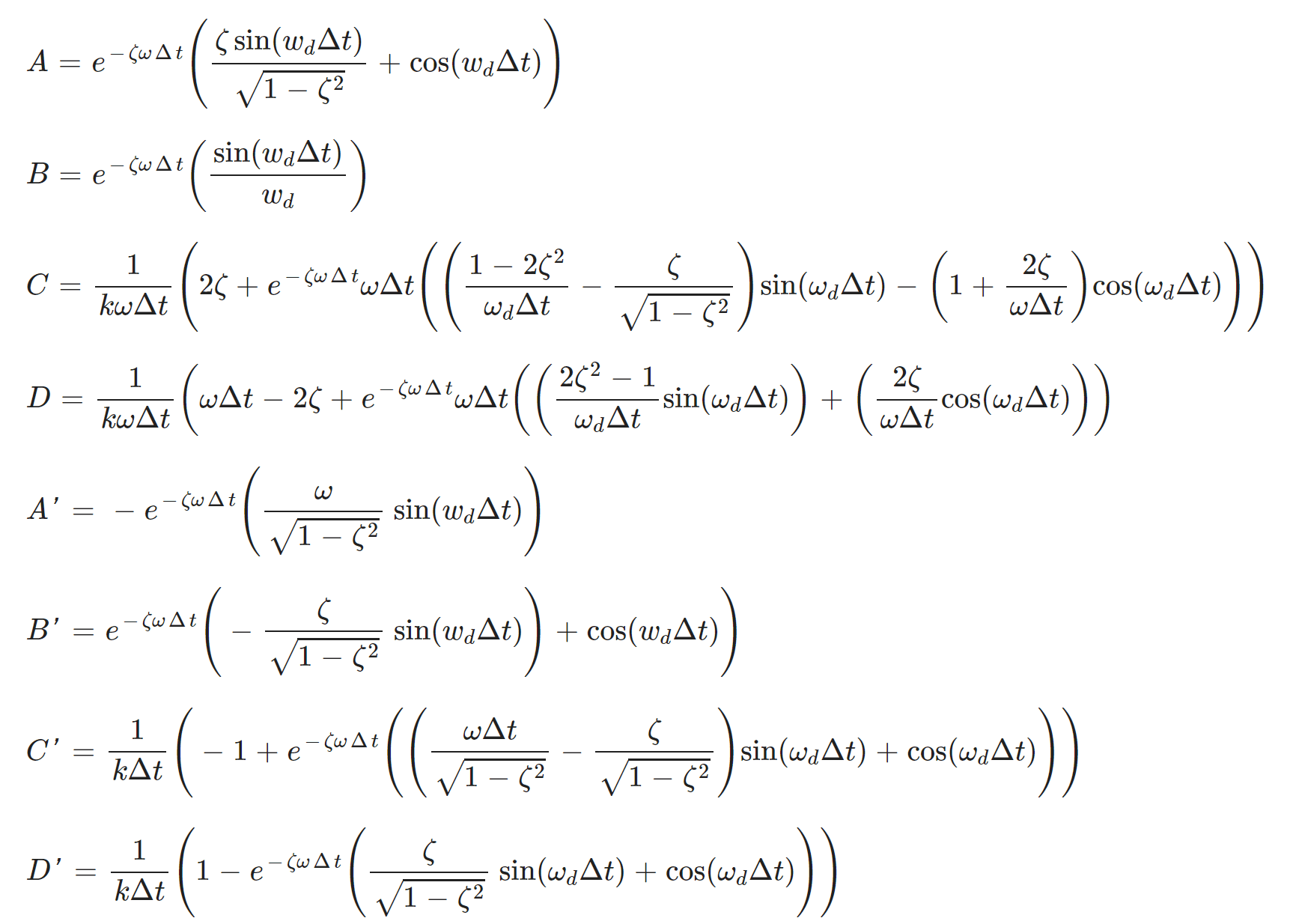
Figure 4.2.2 Constants for the Numerical Method

Application of the Numerical Method

Control Parameters

m

k

ζ

T

Select Pulse Type

Additional Control Parameters

td

Fo

Turn off or on items in the graph legend by clicking on the rectangle in the legend to adjust the scale of the graph automatically

Observations

Numerical method can be used to solve the equation of motion effectively and efficiently. The application of the method was illustrated for different pulses in the previous tool.

Other numerical methods also exist and can be reviewed in many of the available references.